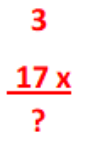Optimale kansen creëren :
door goed en doordacht te rekenen en zo de
Bogey-numbers in het darts te vermijden.
Dat rekenen een heel belangrijk onderdeel is in darten, hebben we wel allemaal gemerkt. Niet alleen om de score kunnen neer te schrijven, de gemiddeldes te berekenen of het check-out-percentage te kennen , maar ook om optimaal kansen te creëren.
Hoofdrekenen is een must voor een goede darter.
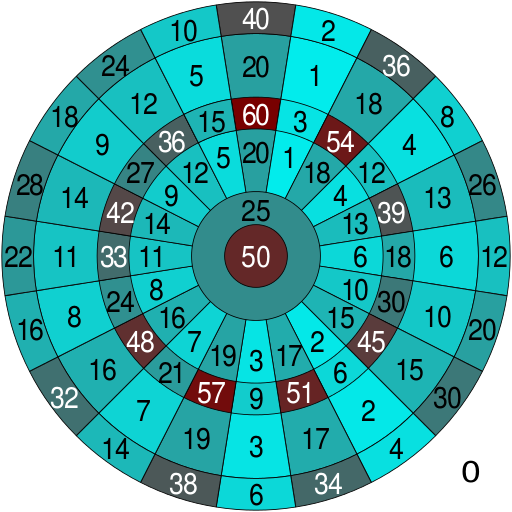
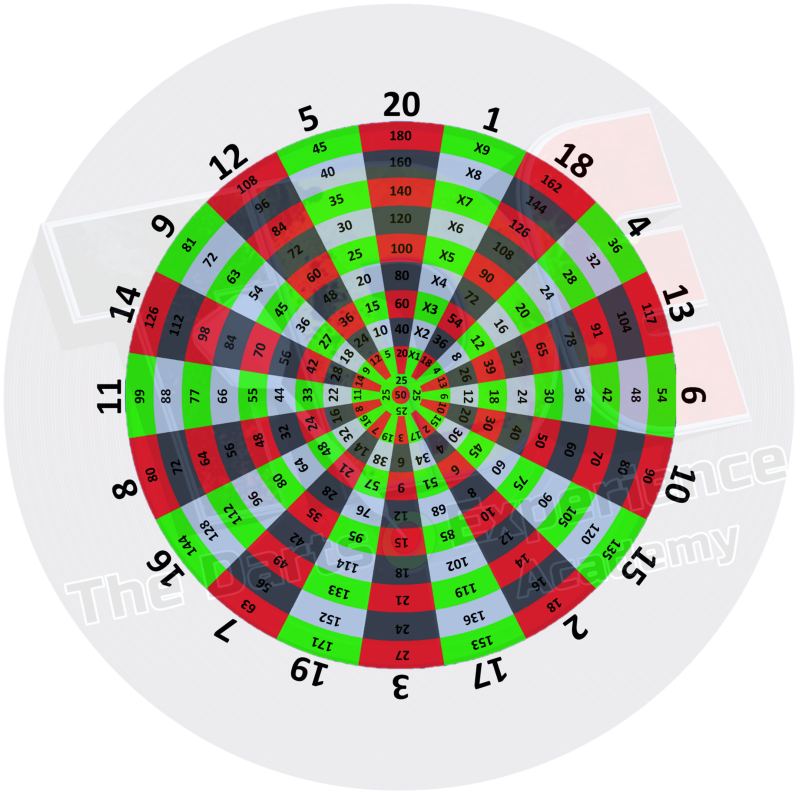
Als darter zal je te maken hebben met optellen , aftrekken , vermenigvuldigen en combinaties van beiden. Hier in ons voorbeeld zie je de verdelingen en scores van de verschillende segmenten op het dartbord.
Hieronder nog even de basis van Optellen, Aftrekken en vermenigvuldigen

Optellen
Snel rekenen begint met snel optellen. Optellen is belangrijk omdat het vaak ook een "tussenstop" is wanneer je vermenigvuldigt. Om snel te kunnen rekenen werk je van links naar rechts in plaats van rechts naar links.
Waarom van links naar rechts?
De meest belangrijke reden om van links naar rechts te rekenen is omdat je getallen van links naar rechts leest en uitspreekt. Omdat je bij hoofdrekenen vaak een aantal stappen moet onthouden, gaat dat makkelijker wanneer je dat kunt doen in de volgorde waarop je de getallen uitspreekt. Als je op papier rekent kies je voor de van rechts naar links methode (d.w.z. je begint bij het meest rechtse en dus het kleinste getal). Maar als je snel wilt rekenen, kun je dat beter uit je hoofd doen. Opschrijven kost namelijk relatief veel tijd! En als je het uit je hoofd doet, is het van links naar rechts veel makkelijker , logischer en sneller, je spreekt trouwens grote getallen ook van links naar rechts uit.
De links naar rechts methode kan het beste worden uitgelegd met een voorbeeld.
Voorbeeld: 57 + 36 = ? (van links naar rechts)
57 + 30 = 87, (tel eerst 30 op)
87 + 6 = 93 (tel daarna 6 op).
93 = antwoord
Optellen van getallen met 2 cijfers
We beginnen met het 'splitsen' van het tweede getal dat je tegenkomt. De manier waarop we splitsen is heel eenvoudig: we nemen de tientallen en de eenheden los. Het getal 32 wordt dus 30 + 2, en het getal 68 wordt dus 60 + 8. Dit 'gesplitste' getal tellen we vervolgens per gesplitst deel bij het eerste getal op. Omdat we van links naar rechts rekenen, beginnen we met de tientallen. Het helpt om de tussenstappen hardop of in je hoofd op te zeggen: in het voorbeeld hier onder zeg je dus: 51, 71, 75.
Voorbeeld: 51 + 24 = ?
Van links naar rechts optellen:
51 + 20 = 71, (tel eerst 20 op)
71 + 4 = 75 (tel daarna 4 op).
75 = antwoord
Met de volgende eenvoudige sommen kun je alvast een beetje aan de van links naar rechts methode wennen.
-
44 + 32 =
-
42 + 24 =
-
51 + 36 =
-
41 + 28 =
-
57 + 32 =
Dit waren relatief eenvoudige sommen: je hoefde geen getallen 'door te schuiven'. Bij de volgende sommen moet dat wel. Je kunt ze gewoon op dezelfde manier oplossen.
Voorbeeld: 67 + 27 = ?
67 + 20 = 87 (tel eerst 20 op)
87 + 7 = 94 (tel dan 7 op)
94 = antwoord
-
57 + 36 =
-
42 + 28 =
-
25 + 36 =
-
54 + 18 =
-
48 + 32 =
Optellen met 3 cijfers
Eigenlijk gaat optellen met drie getallen precies hetzelfde als optellen met twee getallen. Het enige verschil is dat je een extra stap hebt. We beginnen weer met het splitsen van het tweede getal. Omdat dit een getal met drie cijfers is, splits je in honderden, tientallen en eenheden. Die tel je vervolgens in die volgorde bij het eerste getal op. Dus eerst de honderdtallen, dan de tientallen en dan de eenheden.
Voorbeeld: 140 + 154 = ?
140 + 100 = 240
240 + 50 = 290
290 + 4 = 294
294 = antwoord
Probeer jezelf toe oefenen in alleen het opzeggen van de tussenstappen. Je zegt dat hardop of tegen jezelf: 140, 240, 290, 294. Hier staan enkele eenvoudig oefeningen waarbij je telkens twee getallen met drie cijfers bij elkaar optelt.
-
180 + 111 =
-
167 + 121 =
-
157 + 122 =
-
145 + 134 =
-
122 + 170 =
Als alles goed is gegaan heb je de bovenstaande sommen zonder al te veel problemen kunnen maken. We gaan de sommen nu nog een stapje moeilijker maken. In de vorige opgave hoefde je nog geen getallen 'door te schuiven'. In deze opgaven moet dat wel. Natuurlijk gaat dit weer op precies dezelfde manier. Voor het gemak geven we nog een voorbeeld:
Voorbeeld: 177 + 174 = ?
177 + 100 = 277 (tel eerst 100 op)
277 + 70 = 347 (tel daarna 70 op, let op 277 wordt 347)
347 + 4 = 351
351 = antwoord
-
347 + 174 =
-
447 + 278 =
-
744 + 167 =
-
544 + 389 =
-
476 + 355 =
We zijn al bijna bij het eind van de optelsommen. Als het goed is heb je je rekensnelheid al een stuk verbeterd. We gaan nu getallen van 3 cijfers optellen die samen groter zijn dan duizend. Dit gaat natuurlijk weer van links naar rechts. Er is alleen een ding waar je rekening mee moet houden. In ons taalgebruik zeggen we soms twaalfhonderd voor het getal 1200 en veertienhonderd voor het getal 1400. Bij snel rekenen is dat nogal onhandig en kan het snel tot verwarring leiden. Om goed overzicht te houden in het van links naar rechts rekenen, kun je beter zeggen duizend tweehonderd wanneer je het getal 1200 omschrijft dan twaalfhonderd.
Kom je boven de duizend, spreek de duizendtallen dan los uit. Zeg dus duizend tweehonderd in plaats van twaalfhonderd. Dat leidt tot minder verwarring en is makkelijker te onthouden.
-
348+ 785 =
-
479 + 632 =
-
687 + 567 =
-
759 + 468 =
-
369 + 739 =

Snel aftrekken
De methode die we bij het optellen gebruiken, gebruiken we ook bij het aftrekken. We werken opnieuw van links naar rechts en splitsen de getallen in honderdtallen, tientallen en eenheden. 25 lezen we dus als 20 + 5 en 83 als 80 +3.
De links-naar-rechts methode wordt gebruikt voor alle bewerkingen, dus ook voor vermenigvuldigen, delen en aftrekken.
Simpel beginnen
Laten we beginnen met een simpel voorbeeld.
Voorbeeld: 77 - 45 = ? (van links naar rechts)
77 - 45 = 77 - 40 - 5, dus:
77 - 40 = 37
37 - 5 = 32
32 = antwoord
Hieronder vind je een paar oefeningen om dit onder de knie te krijgen.
-
65 - 33 =
-
47 - 11 =
-
78 - 54 =
-
64 - 24 =
-
98 - 62 =
Iets moeilijker
We gaan nu naar het volgende type probleem: 61 - 25 = ? Volgens de methode die hierboven staat uitgelegd kun je dit als volgt uitrekenen.
Voorbeeld: 61 - 25 = ?
we splitsen eerst 25 in 20 + 5, en dan
61 - 20 = 41 (trek eerst 20 eraf)
41 - 5 = 36 (trek daarna 5 eraf)
36 = antwoord
Je kunt deze som ook op een andere manier oplossen. Hierboven hebben we 25 gesplitst in 20 + 5 (=25). Je zou 25 ook kunnen splitsen in 30 - 5 (=25). De bewerking komt er dan als volgt uit te zien:
Voorbeeld: 61 - 25 = ?
we splitsen eerst in 30 - 5, en dan
61 - 30 = 31(trek eerst 30 eraf)
31 + 5 = 36 (tel daarna 5 erbij op)
36 = antwoord
In de eerste stap hebben we 30 van het eerste getal afgetrokken. Dat is 5 meer dan de 25 die we er eigenlijk vanaf moesten trekken. In de tweede stap tellen we die 5 er dus weer bij op. Met deze tweede stap "corrigeer" je dus wat je in de eerste stap teveel hebt afgetrokken.
-
66 - 27 =
-
75 - 38 =
-
72 - 28 =
-
67 - 49 =
-
93 - 67 =
Truc: aftrekken van 100
Het komt vaak van pas om af te trekken van 100. Dat kun je natuurlijk doen op de manieren die hier boven staan, die werken immers prima. Maar er is ook nog een andere methode. Die is als volgt. Trek je meest rechtse getal af van 10, en het linker getal van 9. Dit kunnen we het beste laten zien met een voorbeeld:
Voorbeeld: 100 - 64 = ?
10 - 4 = ...6
90 - 60 = 30
36 = antwoord
Wat je in deze methode doet is niets anders dan 100 splitsen in 10 + 90! Oefen in ieder geval de volgende sommen. Deze vaardigheden heb je nodig om getallen boven de honderd te kunnen aftrekken.
-
100 - 34 =
-
100 - 78 =
-
100 - 43 =
-
100 - 64 =
-
100 - 82 =
Aftrekken met getallen van 3 cijfers
We beginnen eenvoudig. In de volgende sommen hoef je geen getallen 'te lenen' of door de schuiven.
Voorbeeld: 794 - 614 = ?
794 - 600 = 194(trek eerst 600 af)
194 - 10 = 184 (trek daarna 30 af)
184 - 4 = 180 (trek al laatste 4 af)
180 = antwoord
-
453 - 231 =
-
567 - 452 =
-
788 - 435 =
-
589 - 364 =
-
644 - 324 =
Bij de volgende sommen moet je wel getallen doorschuiven, en we beginnen eenvoudig. Stel dat je uit wilt rekenen: 134 - 98 = ? Dan is het handigste om 98 te splitsen in 100 - 2 : Zie verder het voorbeeld.
Voorbeeld: 134 - 98 = ?
134 - 100 = (0)34 (trek eerst 100 af)
34 + 2 = 36 (tel daarna 2 op)
36 = antwoord
Iets meer darts gerelateerd voorbeeld ( deze manier van tellen zal het schrijven makkelijker maken) Pas deze manier toe als de laatste 2 cijfers van het getal dat je dient af te trekken groter is dan de laatste 2 cijfers van je resterende score. zie voorbeeld
441 – 86 = ?
441 – 100 = 341 (trek eerst 100 af)
341 + 14 = 355 (tel daarna 14 op) ( van die waar 14 = 100 – 86)
355 = antwoord
Snel vermenigvuldigen
In het darten gebruiken we de meest eenvoudige manier van vermenigvuldigen (1 x 2 cijfers) en dit gecombineerd met optellen om nadien het totaal af te trekken van de start scores 501, 701 ,1001,… of restscores.
Voorbeeld: 3 x 17 = ?
3 x 10 = 30
3 x 7 = 21
30 + 21 = 51
51 = antwoord
Voorbeeld: 6 x 57 = ?
6 x 50= 300
6 x 7 = 42
300 + 42 = 342
342 = antwoord
Hier volgen een paar darts gerelateerde oefeningen om het bovenstaande te oefenen.
-
(3 x T19) = 3 x (3 x 19) = 3 x .. =
-
(6 x D17) = 3 x (2 x 17) = 6 x .. =
-
(4 x T18) = 4 x (3 x 18) = 4 x .. =
-
(3 x T16) = 3 x (3 x 16) = 3 x .. =
-
(2 x D20) = 2 x (2 x 20) = 2 x .. =
Iets moeilijker en iets minder toepasselijk in darts: 1 x 3 cijfers
We gaan nu naar het volgende type probleem: 6 x 287 = ? Volgens de methodes die hierboven staan uitgelegd kun je dit als volgt uitrekenen:
Voorbeeld: 6 x 232 = ?
We splitsen eerst 287 in 200 + 80 + 7, en dan
6 x 200 = 1200 (spreek uit: duizend twee honderd)
6 x 30 = 180 (tel door: 1300, 1380)
6 x 2 = 12 (tel door: 1390, 1392)
1392 = antwoord
Kom je boven de duizend, spreek de duizendtallen dan los uit. Zeg dus duizend tweehonderd in plaats van twaalfhonderd. Dat leidt tot minder verwarring en is makkelijker te onthouden.
Probeer tijdens de oefeningen zoveel mogelijk door te tellen. Dit helpt je de tussenstappen te onthouden en zorgt ervoor dat je minder fouten maakt. Reken je bijvoorbeeld uit 8 x 178, probeer dan als volgt te tellen (en spreek uit, desnoods hardop): 800, 1360, 1424. Maak je geen zorgen als dit niet meteen lukt; voor hoofdrekenen geldt des te meer: oefening baart kunst!
Lukken deze opgaven niet direct, herbekijk het hoofdstuk optellen nog een keer.
-
5 x 183 =
-
6 x 342 =
-
9 x 986 =
-
3 x 637 =
-
4 x 338 =
Dit waren de basisbeginselen van snel rekenen volgens de van-links-naar-rechts methode. Als het goed is ben je al iets sneller geworden. Sneller word je vooral door te oefenen en de bovenstaande methode consequent toe te passen.
Hier nog even een iets meer darts gerelateerd voorbeeld van 1 x 3 cijfers
3 x 167= ? ook wel één van de meest spectaculaire 9-darters 3 x (T20 , T19, DB)
We splitsen eerst 167 in 100 + 60 + 7, en dan
3 x 100 = 300
3 x 60 = 180 ( deze tellen we bij 300 = 480 )
3 x 7 = 21 ( deze tellen we bij 480 = 501)
501 = antwoord
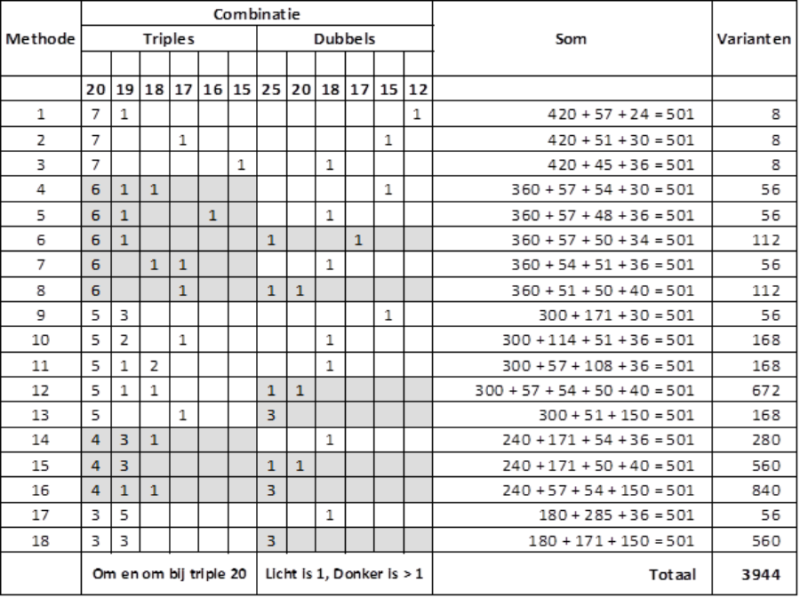
Nu de snelste manier om van 501 naar nul te gaan is de welbefaamde 9-dart finish waaronder de meest voorkomende 180, 180 en 141 checkout is , maar er zijn 18 combinaties mogelijk en tal van verschillende variaties om een 9 darter te gooien. Enig idee hoeveel ? Ontdek het in onderstaande tabel
De worpen mogen in willekeurige volgorde worden gegooid, zolang de laatste maar een dubbel is.
Methodes 6, 8, 12, 13, 15, 16 en 18 bevatten minimaal twee dubbels en kunnen gebruikt worden voor toernooien als de World Grand Prix waar er zowel met een dubbel moet gestart als geëindigd worden.
Dat zijn dus 3944 mogelijkheden om zo snel mogelijk van 501 naar 0 te geraken.
Spijtig genoeg zijn we niet zo accuraat , maar wat kunnen we dan doen als het al misgaat bij die eerste dart , Het is belangrijk dat we optimaal kansen gaan creëren en dit doen we door op voorhand te rekenen zodat we niet op een Bogey-number komen .
Wat is een bogey-number ?
Dit is een score die je niet kan uitgooien met het minimum aantal darts waarbij je normaal een nog hogere score kan mee uitgooien.
Iedereen kent de bogey-nummers, toch? 169, 168, 166, 165, 163, 162, 159
170 is de hoogste score die kan worden gehaald in drie darts, terwijl lagere scores 169, 168, 166, 165, 163, 162 en 159 dat niet kunnen. We leren deze nummers best te vermijden zodat we onszelf de kans kunnen geven om op een hogere getal te eindigen, dit zal ons de kans geven om de leg te winnen met het minimum aantal darts , in plaats van het lagere getal waar bij een extra bezoek aan de okkie vereist zal zijn.
Als je één dart in de hand hebt en een score van 186, zou het een vergissing zijn om naar Treble20 te gooien, omdat Single20 je achterlaat op het bogey-number 166, die je bij je volgende beurt niet kunt voltooien met 3 darts. Het is hier aangewezen om naar T19 te gooien, hierbij kom je op 129 finish of wanneer je S19 gooit op 167 finish laat staan, die je bij je volgende beurt in stijl kunt uitgooien.
Tip: Als je 220 over hebt na twee darts en de T20 is geblokkeerd, schakel dan niet over naar een andere tripel - ze brengen je allemaal op een bogey-number. Gooi in plaats daarvan naar de bullseye ( of dubbele bull) om 170 over te houden.
Maar die zeven getallen zijn niet de enige bogey-numbers. Er zijn eigenlijk 77 die als een bogey-number kunnen worden beschouwd, afhankelijk van hoeveel darts je in handen hebt.
Je weet waarschijnlijk dat je niet naar de T20 moet gooien als je een beurt begint met een score van 119 – bij een S20 kom je op 99 te staan, dit kan niet worden uitgegooid met twee pijlen. Dat maakt 99 een bogey-number met twee pijlen. Als we onze regel volgen dat een bogey-number elke score is die niet in hetzelfde aantal darts kan worden uitgegooid als een hogere score, zien we dat omdat 110 in twee darts kan worden uitgegooid, 109, 108, 106, 105, 103, 102 en 99 allen 2-dartbogey-numbers zijn.
Als we dit uitbreiden naar één dart, aangezien 50 de hoogste checkout is met 1 dart, is alles onder de 50 dat niet in één dart kan worden genomen een 1-dartbogey-number: 49, 48, 47, 46, 45, 44, 43, 42, 41, 39, 37, 35, 33, 31, 29, 27, 25, 23, 21, 19, 17, 15, 13, 11, 9, 7, 5, 3 , (1 =busted en keer je terug naar de resterende score die je bij aanvang van je vorige beurt overhield)
Ik weet zeker dat je deze bogey-numbers al kende, zelfs als je ze niet per se zo noemde. Maar wacht, er zijn er meer!
Als 170 de hoogste score is die kan worden gehaald in drie darts, wat is dan de hoogste score die kan worden behaald in vier darts? Dat zou 230 zijn (170 plus nog een T20). Dus alles minder dan 230 dat niet in vier pijlen kan worden uitgegooid, is ook een bogey-number. Dit zijn de 4-dart bogey-numbers: 229, 228, 226, 225, 223, 222, 219.
Hoe gebruik je deze informatie?
Net als in het bovenstaande voorbeeld met een score van 186 en één dart in de hand, als je twee darts in de hand hebt en een score precies 20 punten hoger dan een van deze bogey-nummers, gooi dan niet naar T20, want de enkele 20 zal laat je achter op een bogey-number. Simpel toch?
Zoals je kan zien, verhoogt elke extra beschikbare dart de bogey-numbers met 60. Aangezien 290 in vijf darts kan worden afgewerkt en 289 niet, is 289 een bogey-nummer met vijf pijlen. Omdat je 350 in zes pijlen kunt nemen, maar niet in 345, is 345 een bogeygetal met zes pijlen. Als je de 7 belangrijkste 3-dart bogey numbers kent : 159,162,163,165,166,168,169 kent dan weet je dat als je daar 60 bij telt dat dat getal een 4-dart bogey number is, als je 2 x 60 bijtelt wordt dit een 5-dart bogeynumber en als je er 60 zou aftrekken krijg je een 2-dart bogey number.
In totaal zijn er 77 bogey numbers leer de 1-dartbogeynumbers van buiten als ook de 3-dart bogeynumbers en dan kan je alle 77 gemakkelijker onthouden en kan je ze leren vermijden in toekomst.
Hieronder vind je alle 77 bogey-numbers:
Dus als je nog maar één pijl in de hand hebt en je hebt nog 369 over , dan gooien we niet naar T20 maar best naar T19 , want als je T20 mist en je raakt S20 hou je 349 over, wat dus een 6-dartbogey-number is, dan wanneer je T19 mist en je S19 raakt hou je 350 over bij je volgende beurt , wat je een kans geeft op een 6-dart finish als je in de volgende beurten een 180 gooit en de Big Fish 170 uitcheckt.
Ga je dit gooien? Misschien niet, maar de kans dat je 349 uitgooit met zes darts is nihil.
Geef jezelf steeds de mogelijkheid
om zulke kansen en grootse momenten te creëren!
Wat betreft de hogere bogey-numbers, neem deze op voor het totale plaatje.
Soms kom je in een situatie terecht waar je bij je eerste bezoek een S20 en tweemaal S1 gooit, hierdoor blijft er bij je volgende beurt 479 over. (Doe niet alsof dit je nog nooit overkomen is.)
De eerste dart van je volgende beurt gooi je naar je T20 maar raakt een S20, waardoor je op 459 komt te staan, wat een 8-dartbogey-number is.
Wat betekent dat?
Het betekent dat je net je kans op een 12 darter hebt verpest - je kunt geen 459 uitgooien in 8 pijlien. Die eerste dart had je naar T19 moeten gooien waarbij je als je de S19 raakt nog 460 zou over hebben, dit kan worden uitgegooid in 8 pijlen met bv. 7 maal T20 en een Dubbel20.
Ik weet dat het absurd lijkt om je zorgen te maken over een 12 darter na het openen met een 22,
maar wanneer je op een bogey-number landt, geef je je tegenstander nog drie darts extra om je te verslaan.
Je denkt misschien dat je met 459 en twee darts in de hand gewoon naar beneden kunt werken en ‘dit later kan herstellen'.
Wees Gerust , Je kan dit niet!
Als je eenmaal op een bogey-number komt, kun je hoge score na hoge score gooien en toch nog steeds op een bogey-number blijven .
Gooi vanaf hier vijfmaal T20 en je hebt 159 met drie pijlen in de hand. Bogey-number. De kans op een 12-darter was verdwenen op het moment dat je de single 20 raakte.
Je zal denken dat die hogere bogey-numbers vrijwel niet relevant zijn omdat je geen topspeler bent en je scoringsgemiddelde er wel voor zal zorgen dat je tegenstander behoorlijk wat meer dan drie extra darts nodig zal hebben in de loop van een leg (en hij zal ze waarschijnlijk direct aan jou teruggeven), maar naarmate je de Tripels en dubbels goed weet te raken , zal het landen op een bogey-number je legs kosten, die jij wellicht had kunnen winnen. Dus doe het niet. Vermijd zelfs de hoogste bogey-numbers en geef jezelf de kans om te winnen met zo weinig mogelijk pijlen.
Belangrijk bij het tellen is dus dat je eigenlijk elke worp onmiddellijk van het resterende getal aftrekt zodat je onmiddellijk weet hoeveel je over hebt en ook zo kan voorkomen om op een van de Bogey-Numbers te komen.
Bv: je eerste worp is S20 dus 501 - 20 = 481over, 2de worp is T20 = 421 over , 3de worp is S20 = 401 over , dus je eerste beurt heb je 100 gegooid en hou je 401 over. Bij de 2de beurt is je eerste worp S20 = 381 over, je 2de worp is T5 (15) = 366, bij je derde worp blik je best terug op de 6Dart Bogey-Numbers zodat je deze kan vermijden en bij je volgende beurt een potentiële 6dart checkout kan creëren.
Bogey numbers 349, 348, 346, 345, 343, 342, 339
Op deze getallen willen we niet uitkomen alsook niet boven de 350 want dat laat ons ook geen mogelijke 6 darts checkout over. De opties voor de derde worp hier zijn 19 want dit laat ons bij het raken van T19 = 309 over of laat ons bij het raken van S19 = 347 over .
Of 16 = T16 brengt ons op 318 en S16 op 350
Of Bull = Bullseye brengt ons op 316 en Single Bull op 341
Zo tellen helpt je dus om optimale kansen te creëren , ook als beginnende darter kan je hier voordeel uithalen , door dit onmiddellijk zo toe te passen moet je je daar nadien niet meer mee bezighouden omdat het reeds geautomatiseerd in je systeem zit .🤫😜🤫